看護学校 受験勉強のポイント「数学」
看護学校受験の数学に関する対策を載せています。
とにかく演習問題をどれだけやったかで力の差がつく科目。
難問はさておき、基本問題を数多くこなそう。
問題文を読んでから解答を出すまでのすばやさも勝負どころ。
数学の出題傾向
数学では、数Ⅰ・数A・数Ⅱが主な範囲である。
ただし、専門学校では数Ⅰ・数Aまでが多く、数Ⅱまで出題するのはごく一部で、出題されたとしても分野の限定があることが多い。
いずれにしろ、中心となるのは数Ⅰとみてよいだろう。
数Ⅰは、因数分解、方程式、不等式、式の計算、関数とグラフ、集合問題など、広くまんべんなく出題されている。
しかし、出題形式のパターンは決まっており、レベルも基本的なもの。
数Ⅰの教科書をもう一度よく復習して、弱点をつぶしておくことが大切だ。
数Aは、「場合の数と確率のみ」、「平面図形除く」といった限定がつくこともある。
数Ⅱのほうは出題も難易度も学校による差が大きいので、必ず過去の問題のチェックをしておくこと。
しかし、一般的に難しくても標準的な範囲のレベルなので、あまり心配することはないだろう。
数Ⅰ・数Aと比べて出題数は減るが、数Ⅱからも代表的な問題が出題されている。
なかでも、微分・積分は比較的が多く、ついで三角関数、指数、対数といったところ。
数Bからは、ベクトルの出題が目立つ。
つまり、数Ⅰ・数Aはまんべんなくマスタ一しておかなくてはならず、数Ⅱ・数Bも教科書の代表的な問題はクリアしておくことが必要だ。
数学の受験勉強・対策のポイント
数Ⅰ・数A
看護系の数Ⅰはとにかく、「基本問題」は全て出る可能性がある。
それなりに時間はとるが、あまり難問に取り組む必要はないので、確実に教科書程度の問題をこなし、解けるようにしておくこと。
かなり出題数も多いので、速くミスなく、を心がけよう。
それにはなんといっても、数多くの問題をこなすしかないだろう。
数と式の対策
因数分解は頻度No.1といってよい分野。
「~を因数分解しなさい」というストレートな出題以外にも因数分解の問題は多数出題されている。
また二次関数・三次関数とグラフでも因数分解の技術は必要。
公式を確実に覚えておこう。
また、係数を有理数の範囲(√のある数を係数にもたない)で考えるか、実数の範囲(2乗してマイナスの符号になる数を係数にもたない)で考えるか、に注意。
(何も指示がない場合は有理数までで止めてよい。)
方程式と不等式の対策
因数分解をして解くか、解の公式を使って解く。
二次方程式の解の公式
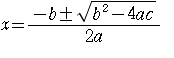
は重要。
この公式を使って解を求めてから因数分解をすることができる。
解と係数の関係も重要。
すなわちα、βを2つの解とするとき、
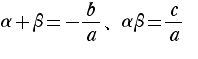
二次関数の対策
二次関数とそのグラフではグラフの移動についての問題に注意。
放物線の向きと移動の値が、最大(小)値、頂点の座標、軸の方程式とからめて出題されている。
三角比の対策
ごく基本的な出題がみられる。
主な三角比の値と公式はきちんとおさえておくこと。
集合と論理の対策
「裏」「逆」「対偶」というような用語の意味や命題の論理記号を誤らないようにすること。
場合の数と確率の対策
順列・組合せは、言葉と記号を正しく覚えていることがなによりも大切。
n個の異なるものの中から7個を取り出して並べるのが順列で、nP7で表す(n=7のときn!)。
n個の異なるものの中から順序は考えずに取り出すのが組合せで、nCrで表す。
確率では、さいころを投げる、異なる色の玉を取り出すなどの問題が頻出だ。
数Ⅱ
高次方程式では三次方程式の解と係数の関係、すなわち、
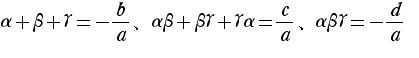
を使う問題の出題も目立つ。
円の方程式では円と直線や放物線の交点の座標を求めさせる問題がよくみられる。
円の方程式は展開した形では、x、yの二次方程式で、![]() と
と![]() の係数が等しくxyの項をもたない、
の係数が等しくxyの項をもたない、
![]()
の形でかけるものだ。
三角関数、指数関数、対数関数では暗記すべき公式が多くある。
まず定理・公式を確実に覚えてから、それを使えるようにしておくこと。
これらは学校によって出題にばらつきが多い分野なので、過去の出題をきっちり確認しよう。
また、関数のグラフの形はおさえておくこと。
指数関数と対数関数は互いに逆関数で、グラフは線対称になっている。
もし係数とグラフの傾きの関係を忘れた場合は、わかりやすい値を代入してみるとよいだろう。
微分・積分の出題のパターンはかなり限られていて、基礎的なものである。
特に接線の方程式を求める、接線と曲線に囲まれた部分の面積を求める、という問題が頻出している。
数B
数列、ベクトルが範囲。
数Bの出題はほかにもまして学校による差が大きいので、必ず志望校の過去の傾向を確認すること。
数列は公式の多い分野なので、公式を覚えるときは丸暗記ではなく、その公式がどうやって導かれるかを理解しておくこと。
ベクトルの分野では、ベクトルの成分による演算、直線の方程式、平面の方程式、ベクトルの内積が重要だ。
出題形式としては、単純なベクトルの演算から、1直線上にある点の成分を求めさせる問題など、基礎的なものが多い。
そのほか、ある条件を満たす点の軌跡の式を求めさせる問題、直線と直線の距離、2直線の交点やそれを含む平面の方程式を求めさせる問題などが、やや高度なものとして出題されている。
おすすめの記事
⇒ 看護学校 受験勉強「英語」のポイントはこちら
⇒ 看護学校 受験勉強「国語」のポイントはこちら
⇒ 看護学校 受験勉強「理科」のポイントはこちら
⇒ 看護学校 受験勉強「小論文」のポイントはこちら